Память об институтских предметах (1)

Автор: Михаил Глебов, январь 2004

Ниже я дополнительно (коли к слову пришлось) приведу несколько фрагментов насчет моей учебы в Инженерно-строительном институте на грани 1970-80-х годов. Я заканчивал привилегированную "теоретическую" группу, которая до такой степени погрязла в никчемных интегралах, что осталась в девственном неведении относительно множества действительно важных вещей. И это очень больно сказалось при переходе от курсовых работ к реальному проектированию.

Бей профессоров, они гадюки,
Они нам замутили все науки!
(Фольклор Физфака МГУ)

[...] Ежедневно в расписании значилось по четыре пары, редко по три, т.е. по 6-8 часов, или полный рабочий день, - куда, естественно, не включалась домашняя работа над многочисленными курсовыми. В результате нормальное усвоение материала было попросту невозможно, ибо человеческий мозг, как и любое шоссе, имеет предел пропускной способности, причем у большинства он расположен весьма низко. Или, говоря иначе, наши стаканы оказались слишком малы для потока вливаемой туда воды, большая часть которой поневоле расплескивалась зря. А так как любое учение ведется последовательно и каждая новая тема опирается на усвоенную предыдущую, всякий пропуск в тылу болезненно отражался на дальнейшем понимании предмета, так что ко времени получения дипломов мы имели в головах густую и плохо переваренную кашу.

С другой стороны, та несъедобно-заумная форма, в которой большей частью нам преподавался материал, кратчайшим путем наводила студентов на мысль о его не то что ложности, но практической непригодности для любого реального дела. Ибо человек, обладающий здравым рассудком, прежде чем заняться чем-нибудь, в особенности серьезным и трудоемким, задает вопрос "зачем?" и если не получает на него удовлетворительного ответа, проникается скептицизмом. - К сожалению, ни школа, ни институт по громадному большинству пунктов не могли ответить ученикам на этот основополагающий вопрос. Я уже неоднократно затрагивал эту тему и теперь поневоле возвращаюсь к ней снова. В школе, от которой требовалось дать ученикам общее образование, т.е. твердое понимание всех азов, дети были завалены Монбланом фактов, пригодных для специального, профильного образования. В институте же, предназначенном как раз для этого последнего, напротив, предметы расползались далеко вширь, так что теряли всякую связь с той жизненной обстановкой, в которой предстояло работать выпускникам.

Если институты созданы для того, чтобы готовить профессионалов по конкретным специальностям, их учебные программы обязаны решать как минимум две цели: (1) дать студентам твердое качественное понимание основ их будущей профессии, т.е. заложить в их головах надежный фундамент, и (2) адаптировать их к реальной жизни, чтобы они не приходили на свои рабочие места белыми воронами, а органично вливались в общее русло трудовой деятельности.

Применительно к профессии инженеров-строителей первый пункт означает прежде всего понимание работы конструкций, столь же важное для проектировщика, как музыкальный слух - для скрипача. Инженер задумывает и создает на бумаге конструкции, которые, будучи воплощены в жизнь и затем обвалившись, не только причиняют огромный материальный ущерб, но и чреваты гибелью многих людей. Следовательно, его деятельность нельзя считать простым бумагомаранием (как это распространено в народе), но скорее работой сапера, который ошибается только один раз. В конструкциях же, как и в любом человеческом деле, есть вещи важнейшие, фундаментальные, и есть очень много второстепенных. Эти последние без конца меняются в зависимости от конкретных условий; но первые остаются незыблемыми всегда, и вот их-то как раз и следует знать назубок. Под этим я понимаю не тупое заучивание формул и правил (хотя и без этого нельзя обойтись), но чисто качественное понимание того, что происходит внутри данной конструкции: какие усилия там действуют, как они распределены и где, вследствие этого, скрываются опасные места, на которые нужно обратить внимание в первую очередь. Лидером среди дисциплин такого рода, без сомнения, является Сопромат, к нему примыкают Строительная механика, Железобетонные и Стальные конструкции (о чем достаточно говорилось выше). И если студент хорошо усвоил самую соль этих предметов, он уже по факту является инженером, хотя бы не производил никаких реальных расчетов.

С другой стороны, инженер трудится не в безвоздушном пространстве, а в очень конкретных условиях, определяемых уровнем развития строительной индустрии, сложностью возводимых зданий, средней квалификацией проектировщиков, нормативной базой, которой они обязаны придерживаться, правилами черчения и т.п. Это вроде как в танцах: нельзя танцевать абстрактно, вообще, разве только дома перед зеркалом; но если ты пришел на бал и объявляют вальс, нужно придерживаться правил вальса, даже если они почему-либо кажутся тебе далекими от совершенства, а когда объявили мазурку, надо танцевать мазурку. Равным образом и молодой инженер, явившись на свое место в проектной конторе, должен не хлопать глазами по сторонам (ибо в этом случае он оказывается бесполезен и требует дополнительного обучения за счет этой конторы), а почти сразу вступить в дело хотя бы на подсобных ролях. Ибо на бал приходят уже обученными, бал - это не танцкласс, а проектное бюро - не студенческая аудитория, у каждого из них - свои задачи, и их не следует путать.

Итак, в освоении любой профессии существуют две вершины, две болевые точки - понимание теоретических основ и владение практическими навыками. Все остальное, коему нет числа, приходит к специалисту со временем, причем к каждому - по его конкретным потребностям. Если, положим, я занимался проектированием атомных электростанций, меня вовсе не касались подробности возведения жилых домов, а те инженеры, что проектировали дома, не нуждались в знании правил для АЭС. Ибо всего на свете знать нельзя и даже категорически не нужно, поскольку лишние знания, не применяемые к делу, только напрасно засоряют память. Вот почему институтские программы обязаны быть гораздо более краткими и сфокусированными на "болевых точках", а практические занятия - иметь в виду современные реалии проектных организаций.

Однако опыт моей учебы в МИСИ демонстрирует противоположную ситуацию. Азы нам, конечно, давали, но в общем потоке информации, так что они проскакивали через сознание едва замеченными. Что же касается "практики", солидные мэтры даже брезговали задумываться о такой прозе. В результате мы (как и в школе) оказались по уши завалены ненужной и непригодной к делу, а между тем очень сложной для понимания информацией; и поскольку время поджимало, а экзаменаторы остерегались свирепствовать, эти недоученные темы на другой день после сессии благополучно выветривались из головы.

Здесь мне могут сделать справедливое замечание: ведь инженеров-проектировщиков готовили группы КПГС (конструкторские), а твоя "Теория сооружений" как раз и предназначалась для всякой зауми, чего же тут жаловаться? - Во-первых, близко общаясь с ребятами из КПГС, я не видел между нашими программами принципиальной разницы. Во-вторых, намерение изучать сложные вещи нисколько не отменяет необходимости изучения более простых, подобно тому как строительство третьего этажа не отменяет надобности в уже готовых втором и первом. Всякая заумь, чтобы быть понятой, должна опираться на твердый фундамент усвоенных базовых знаний; без этого она фатально повисает в воздухе и делается пустым нагромождением формул. В-третьих, дерево любой науки ветвится тем сильнее, чем дальше уходит от ствола, и потому всякая заумь очень конкретна, ибо принадлежит к одной из бесчисленных тонких веток. Но даже если студент твердо решился посвятить свою жизнь научным исследованиям, где гарантия, что предмет его деятельности окажется как раз этим самым? С гораздо большей вероятностью он устроится при другой кафедре и займется другой темой, и там будет совсем иная заумь, а к чему тогда он учил прежнюю? В-четвертых, ученые существуют не для того, чтобы витать в эмпиреях, а чтобы решать наиболее сложные практические задачи, которые им перепоручают рядовые конструкторы. Следовательно, ученый должен уметь разговаривать с ними на одном языке, а для этого ему необходимо понимать ситуацию и уж во всяком случае не быть белой вороной. Не беря того распространенного случая, когда он с треском вылетает со своей кафедры и отныне вынужден заниматься проектированием на общих основаниях.

Наиболее вредный перегиб институтской программы заключался в излишнем внимании к математике: она давалась нам в объемах, многократно превышавших самые смелые научные потребности в строительстве, которое все-таки не есть ядерная физика. Эту тему я уже затрагивал, и приведу оттуда следующую выдержку:

На втором и третьем курсах этот предмет вел доцент Ш. - большой, неуклюжий, нестриженый человек не от мира сего, в пыльной кофте и с виноватой улыбкой Пьера Безухова на лице, хорошо что не злой; он, повернувшись к доске, бормотал что-то невнятное и писал формулы, затем спохватывался, исправлял в формулах буквы, где-то подчеркивал, зачеркивал и, нисколько не заботясь о контакте с аудиторией, молол эту чушь в свое удовольствие до конца "пары". Здесь были дикости типа преобразования плоскости в точку, а точки в пространство, и прочая подобная заумь. Никто из нас не мог законспектировать его бреда, а учебника к этому курсу не было, ибо Ш. отважно разработал его сам. - По счастью, в итоге от нас потребовался не экзамен, а только зачет. Вся группа собралась в коридоре, староста собрал зачетки и нагло зашел с этой кипой к Ш.; о чем они там беседовали, я не знаю, но в итоге зачеты оказались заочно поставлены всем.

Этот пример великолепно подтверждает старую как мир истину, что крайности сходятся, и ставка на чрезмерную "ученость" в реальной жизни оборачивается полным невежеством. Если бы Ш. использовал выделенное ему время на проработку базовых начал высшей (и не только высшей!) математики, это было бы гораздо полезнее для всех. Но он попытался вбить в свой курс максимальное количество заумных тем, невесть кому нужных, которые в результате пролетали без понимания и, следовательно, не оставили в наших умах никаких следов. Не беря уже его полной педагогической непригодности.

Важнейшая наука любого инженера - сопромат - читалась на третьем курсе, т.е. всего два семестра. Ее вел странный мужичонка Г., курносый и низкий ростом; он всегда ходил в клетчатой рубашке и в перерывах, зайдя в уборную, рассказывал студентам матерные анекдоты. Не думаю, что такое поведение укрепляло его престиж. Его лекции были вразумительны, но главное счастье заключалось в существовании двух хороших учебников, на которые мы главным образом и рассчитывали. Многие темы промелькнули, словно метеоры на ночном небе, курсовых было мало, а в результате сопромат почти незаметно канул в небытие. По-настоящему же я схватился за учебник, лишь когда вышел на работу.

Если сопромат изучает распределение усилий в каком-либо одном месте конструкции и, следовательно, озабочен прочностью этого места, строительная механика рассматривает всю конструкцию в целом - растекающиеся по ней усилия, деформации и т.п.; ясно, что эти предметы являются двумя половинками единого целого. К нашему счастью, клетчатый мужичонка хотя бы не испакостил свой предмет прогрессивными нововведениями и читал лекции, как у себя в колхозе, т.е. доступно и по старинке. Но элегантный профессор N придерживался иных взглядов, результатом чего стали две взаимно противоположные глупости.

Дело в том, что почти всякая строительная конструкция, состоящая хотя бы из двух жестко скрепленных элементов (к примеру, колонна и опирающаяся на нее балка), требует удивительно долгого и нудного расчета; эта тема затрагивалась выше. Ситуация здесь почти та же самая, что в арифметике при нахождении синуса какого-либо угла или извлечении корня: ничего принципиально сложного нет, но жалко потраченного времени. Именно поэтому и там и тут еще в XIX веке были созданы таблицы, позволяющие без лишних хлопот отыскивать значение любого синуса, корня - а равным образом и формулы для расчета строительных схем не слишком сложной конфигурации. Если же человек безрассудно хотел все-таки рассчитать такую конструкцию сам, к его услугам были два гнусных метода - метод сил и метод перемещений, посредством которых он уже через полдня, изрисовав эскизами кучу бумаги, получал для тех двух элементов все необходимые данные (если, конечно, по дороге не ошибся). Эти "методы" по своей сути были элементарны, но требовали громоздких вычислений и сверхъестественной аккуратности. Владение ими не прибавляло студентам реального понимания предмета, как не прибавляли этого в математике и вереницы головоломных задач. - Вот в таких дурацких расчетах и состояли курсовые задания по строительной механике.

Если же вам попалась не элементарная схема на два-три элемента, а какое-нибудь высотное здание, где этих элементов многие десятки, если не сотни, - означенные "методы" угрожают многомесячным каторжным трудом, который действительно производился большими коллективами расчетчиков до наступления компьютерной эры. Компьютер же поступает просто: избавленный от человеческой неряшливости, он легко создает грандиозные системы линейных уравнений, которые сам же и решает, и выдает инженеру готовые результаты, так что этот последний сам уже практически не затрагивает расчетную часть. Но профессору N пришло в голову двинуться вслед за компьютером и излагать нам материал не с позиции его здравого понимания, а следуя тем системам линейных уравнений, которые служат лишь промежуточным математическим инструментом и ничего не объясняют по существу. В Вильнюсе же, как я слышал, пошли еще дальше, заменив эти уравнения (хоть как-то привязанные к реальной схеме) уже совершенно абстрактными матрицами, с которыми, собственно, и оперирует мертвый компьютер. Результат же везде вышел один: пожертвовав смыслом задачи в пользу чисто технических средств ее решения, прогрессивные профессора (помимо премий и научных лавров) добились лишь полного непонимания студентами основ своего предмета, который, стало быть, оказался прочитан ими зря.

Однако здесь были еще цветочки, в чем мы явственно убедились при переходе на 4-ый курс. Словно вся академическая премудрость стопудовым молотом обрушилась на наши головы. Жирный профессор Л. два семестра читал нам убийственную Теорию упругости, которая была воспета мною несколько выше, так что теперь я поберегу порох. Здесь в каждом уравнении сияли многоэтажные дифференциалы и интегралы, понять смысл которых было невозможно хотя бы по причине отсутствия толкового учебника. Точнее, один толковый учебник был - зарубежный, и ребята кое-как добывали его в магазинах технической книги, но Л. будто нарочно читал лекции таким образом, что они нигде с тем учебником не сходились. В результате даже величайшие отличники и зубрилки хлопали глазами и раскрывали рты, словно рыбы, вытащенные на воздух. Я же, не растерявшись, двинул в бой свою испытанную гвардию - материалы XXV Съезда КПСС, где при очень горячем желании можно было сыскать некоторые реверансы в сторону Теории упругости. Дифференциалы не смогли противостоять большевистскому натиску и дружно капитулировали, украсив мою зачетную книжку очередной пятеркой. Другие ребята также врали кто во что горазд, и этот предмет благополучно пролетел у нас из одного уха в другое.

Но вслед за Теорией Упругости явились невыносимые Пластинки и оболочки, посвященные изучению всевозможных мембран и куполов. Вел этот предмет великий профессор Р. - длинный, лысоватый и бедно одетый старик, выпустивший несколько гениальных учебников, которые он один, видимо, и смог прочесть до конца. В голове у него теснилось очень много извилин, но они никак не могли разобраться между собой по порядку. Он обладал уникальной способностью сложно излагать даже простейшие вещи. А поскольку действительно простых вещей в его предмете найти было трудно, Р. на лекциях приходил в хорошее настроение, улыбался, копал в носу и очень просил всех не расстраиваться. Он рисовал на доске купол, и вырезал из него маленький лоскуток, и размашисто вычерчивал этот трехмерный кубик по соседству, и прикладывал к нему различные усилия, и когда убеждался, что это нам покамест понятно, решительно исправлял положение, запачкав остальную часть доски неведомо откуда набежавшими дифференциалами. В аудитории между тем начинался шорох, кто-то с треском выдирал листок, чтобы играть в "морской бой", и Р. с блаженной улыбкой, заплетаясь ногами вокруг стула, извинялся, что в самом начале перепутал дифференциалы местами, и оттого у него теперь вышла ерунда, и он просит не расстраиваться и дома самим написать все сначала как следует, чтобы лекция была полной.

Однако "написать как следует" эти формулы удавалось редко, ибо они почти всегда были несимметричны. Для наглядности возьмем известные каждому школьнику примеры:

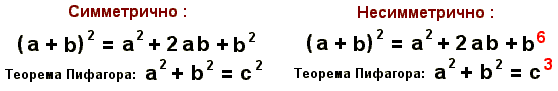
Даже не вникая в суть написанного, вы сразу насторожитесь, заметив шестую степень в первом примере и третью во втором, потому что они как бы нарушают гармонию и "выпадают из ряда". Вы интуитивно чувствуете, что здесь их не должно быть, и чувствуете верно, поскольку правильные решения чаще всего имеют гармоничный и аккуратный вид. Но в "Пластинках и оболочках" большинство формул получалось благодаря многократному интегрированию, а этот процесс таков, что дает кособокие и заранее непредсказуемые результаты. Если же интегрированию подлежит длиннейшая формула на десять членов, в итоге их получается как минимум двадцать, притом все разные, и никакой здравый смысл не подскажет вам, есть ли тут ошибка, и если есть, то где именно.

Однажды, собравшись начать "новую жизнь", я храбро решил выполнить ближайшую курсовую работу по "Пластинкам и оболочкам" как следует, т.е. без списывания и прочих махинаций. Пластинка же была прямоугольная, с разными типами опирания по четырем сторонам и несколькими вариантами нагрузок. Целый вечер я как последний идиот гонял интегралы, перепортил вагон бумаги и поскольку в результате получил ерунду, назавтра отправился консультироваться к аспиранту, который вел у нас практические занятия. Моя суровая решимость добиться толку повергла аспиранта в грустное настроение; он дал несколько ценных указаний и поскорее удалился. Вернувшись домой, я проделал работу сызнова и опять получил ерунду. Тогда, чтобы не расстраивать аспиранта, я устроил опрос в группе, и ребята наконец признались, что ерунду получили все, но поскольку из сопромата могли прикинуть приблизительные значения, то их и вписали в ответ, а путаницу интегралов оставили лежать так - в уверенности, что наш аспирант поленится проверять их от строчки к строчке. И я эмоционально хлопнул себя по лбу, и на этот раз так и не начал "новую жизнь". - Спрашивается, кому и какая польза была от таких занятий?

Однако ужасы этого предмета в значительной мере скрашивались расхлябанным добродушием Р., который от избытка благости готов был раздать пятерки всем желающим, и даже бежать за ними следом и всовывать насильно. От нас требовалось только попасть на экзамене лично к нему, а не к его ассистенту. И я, верный своей методике, нагло ворвался в аудиторию первым, и взял самый первый по счету билет, и почти не готовился, и пошел прямо к Р., и патетически рассказал ему о значении пластинок и оболочек в деле строительства коммунизма. И Р., едва не пустив слезу от столь высокой оценки его предмета, поставил мне "отлично" и рядом широкую невразумительную подпись. Хотя я бы, по совести, не поставил себе и кола.